Problem Statement: https://leetcode.com/explore/challenge/card/june-leetcoding-challenge-2021/606/week-4-june-22nd-june-28th/3790/

After solving a few similar problems, I see a pattern here. Whenever you want to do an exhaustive search. First write a recursive brute force solution, which will definitely fail because of high time complexity. After that memorize the answer for a state so you don’t have to calculate a particular cell again.

In this problem, we have given a grid, an initial position, and the number of steps that can be taken and we have to find how many times we will go out of the grid. So here if we do a brute force and explore all the paths. The complexity here will be O(4^(row*col)) because there are row*col cells and for every cell, there are 4 paths.

The constraint says row and col can max 50. So in the worst case, we will do 4^2500 =

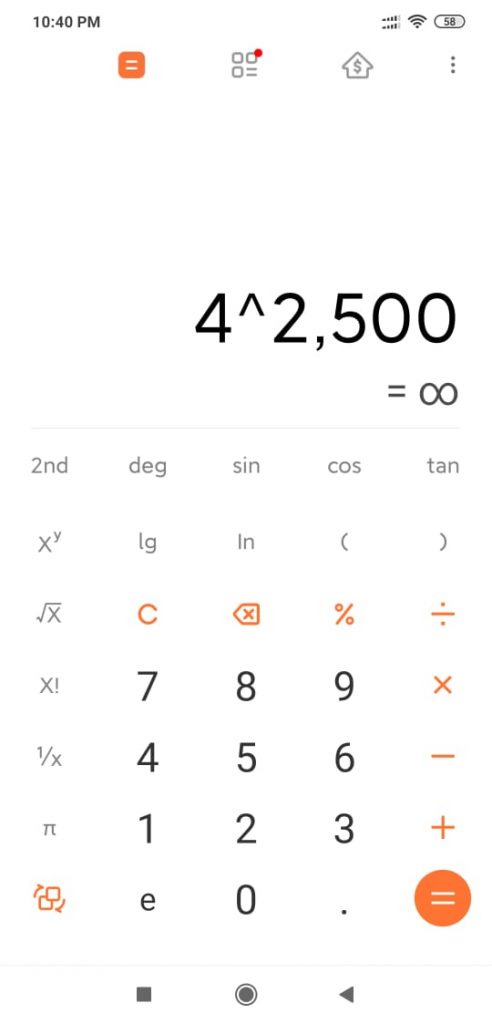
So this will definitely will give time out. Now we have to memoize the cell’s response so we don’t have to calculate again. If you think a cell’s input will be total steps left. So if we are at (1,1) the answer will be different for 2 steps left, 1 steps left, and 10 steps. So every cell will have 50 input because as per the problem statement max number of moves is 50.

So if we save the answer for all cells, and every cell will have 50 inputs. The total calculation will be 50*50*50 = 125000 Iteration. Can be solved.

Let’s memoize!!