Problem statement

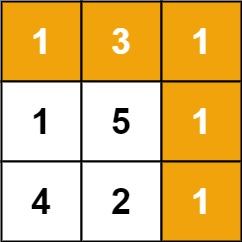
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

If you notice this problem, from a position we can move right or down. Let’s go through my thought process. First, can I select the best path from a given position? The possible way is selecting greedily. But this will fail in the first example itself, we are picking 3 instead of 1 from 1st position.

So I know, greedy won’t work. Can I do an exhaustive search? Let’s check the complexity. For every position, there is 2 path. so O(2^N).

The complexity is high but that’s the only thing I know, let’s go for it.

public int recurse(int [][] grid, int i, int j)
{
     // If reached the last element return the element
     if(i == grid.length - 1 && j == grid[0].length - 1)
    {
        return grid[i][j];
    }
    int min = Integer.MAX_VALUE;
    // if right is valid path visit 
    if(i + 1 < grid.length)
    {
        min = Math.min(min, recurse(grid, i + 1, j));
    }
    // if down is a valid path visit
    if(j + 1 < grid[0].length)
    {
        min = Math.min(min, recurse(grid, i, j + 1));
    }
    return min + grid[i][j];
}

In the above code, I’m exploring all possible paths. If we create a recurse graph for this. It will look like this.

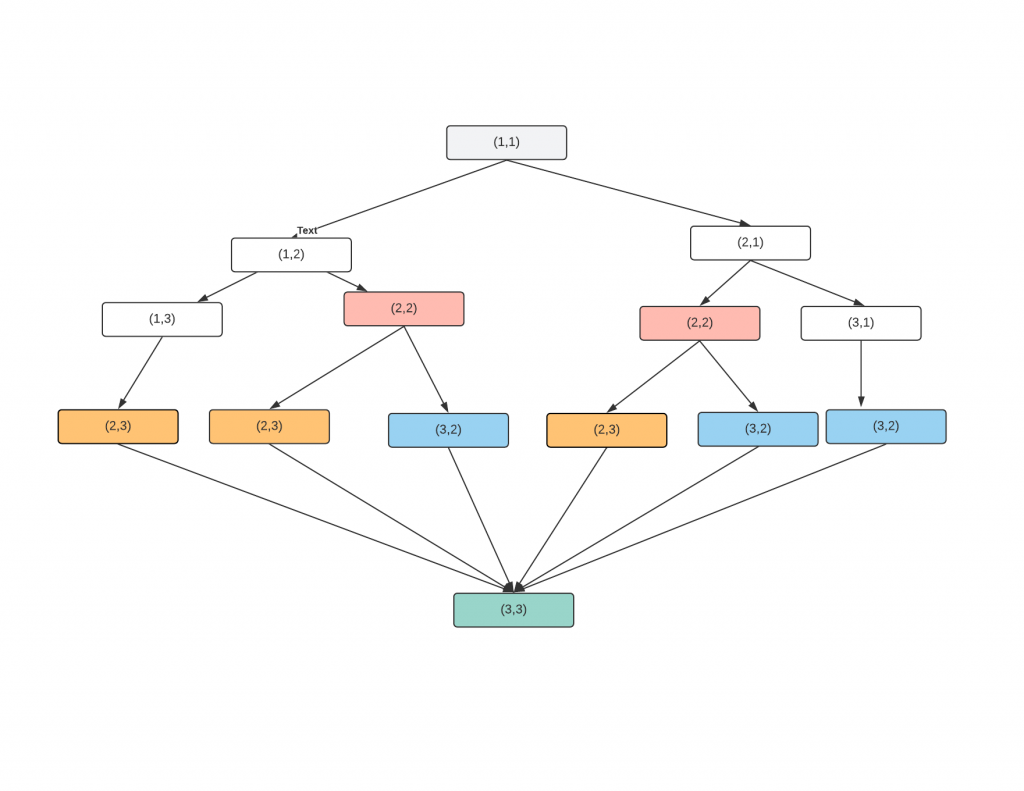
If you see, we are calculating the same node multiple times, if I already calculated for node(i,j), there is no need to calculating again. Let’s introduce a caching layer, which will save the answer for (i,j) if the we need it again, we can just return that value.

// Initialize with all one 
int cache[][];    
public int recurse(int [][] grid, int i, int j)
    {
        if(i == grid.length - 1 && j == grid[0].length - 1)
        {
            return grid[i][j];
        }
        // If once calculate just return it
        if(cache[i][j] != -1)
        {
            return cache[i][j];
        }
        int min = Integer.MAX_VALUE;
        if(i + 1 < grid.length)
        {
            min = Math.min(min, recurse(grid, i + 1, j));
        }
        if(j + 1 < grid[0].length)
        {
            min = Math.min(min, recurse(grid, i, j + 1));
        }
        cache[i][j] = min + grid[i][j];
        return cache[i][j];
    }

After caching the result the graph will look like this, where the colored nodes are calculated only once and returns the same result next time if asked.

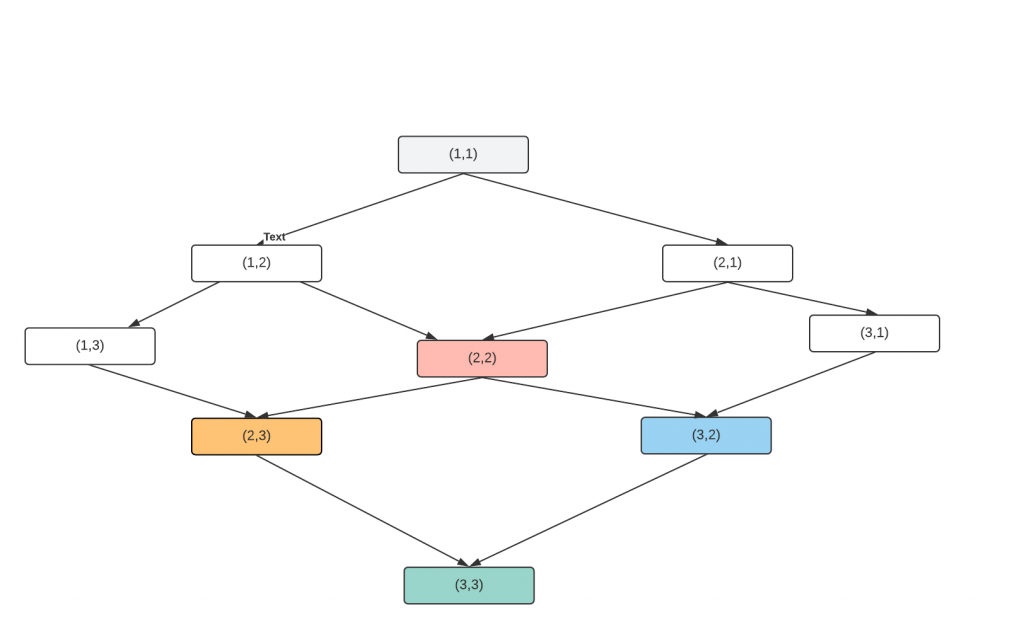
Now the complexity is O(m*n) because we are visiting each node only once.