Problem Statement

To be frank, as I read the problem I realized it is a BFS problem. Let’s see what was my thought, we have to count the number of steps to reach the final string, this denotes we have to traverse the intermediate nodes. We cannot directly jump to the final string and apply some formula to get minimum steps. My second thought was can I change the final string and try to reach “0000”. We can try this but finding the minimum number of steps from this approach is difficult.

Finding a minimum number of steps from one position to another which has intermediate states, BFS was my next thought.
Given a string with 4 characters where each character is between 0-9. So there are 10^4 possibilities. To convert a problem to a graph problem we want Nodes and Edges. Let’s convert this to a graph problem by denoting a single string as a Node. i.e “0000” is one Node, “1000” another.

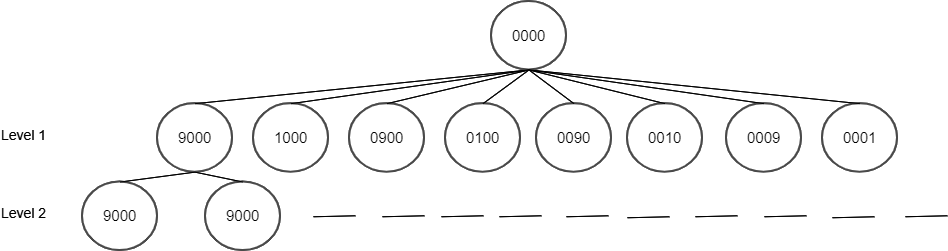
In step 1 we can reach all the nodes in Level 1, in 2 steps all the Nodes in level 2. This is a BFS, we have to find at what level our target Node is present and avoid visiting the already visited node. Along with that, the problem statement provides some Nodes as Invalid. We should not traverse these nodes further.

	class Node
	{
	int a,b,c,d;
	public Node(int x,int y, int z, int k)
	{
	a = x;
	b = y;
	c = z;
	d = k;
	}
	public Node(Node n)
	{
	a = n.a;
	b = n.b;
	c = n.c;
	d = n.d;
	}
	public String toString()
	{
	return a+""+b+""+c+""+d;
	}
	}
	class Solution {
	public int openLock(String[] deadends, String target) {
	HashSet<String> deadEnds = new HashSet<String>();
	for(int i=0;i<deadends.length;i++)
	{
	deadEnds.add(deadends[i]);
	}
	Node start = new Node(0,0,0,0);
	if(deadEnds.contains(start.toString()))
	{
	System.out.println("start");
	return -1;
	}
	if(start.toString().equals(target))
	{
	return 0;
	}
	return bfs(start, target, deadEnds);
	}
	public int bfs(Node start,String target, HashSet<String> deadEnd)
	{
	LinkedList<Node> queue = new LinkedList<Node>();
	HashSet<String> visited = new HashSet<String>();
	queue.add(start);
	visited.add(start.toString());
	int level = 0;
	while(queue.size() > 0)
	{
	int size = queue.size();
	for(int i=0;i<size;i++)
	{
	Node temp = queue.poll();
	if(temp.toString().equals(target))
	{
	return level;
	}
	/// a Updated
	Node temp1 = new Node(temp);
	temp1.a = increment(temp.a);
	if(!deadEnd.contains(temp1.toString()) && !visited.contains(temp1.toString()))
	{
	//System.out.println(temp1);
	visited.add(temp1.toString());
	queue.add(temp1);
	}
	Node temp2 = new Node(temp);
	temp2.a = decremet(temp.a);
	if(!deadEnd.contains(temp2.toString()) && !visited.contains(temp2.toString()))
	{
	//System.out.println(temp2);
	visited.add(temp2.toString());
	queue.add(temp2);
	}
	// b updated
	Node temp3 = new Node(temp);
	temp3.b = increment(temp.b);
	if(!deadEnd.contains(temp3.toString()) && !visited.contains(temp3.toString()))
	{
	//System.out.println(temp3);
	visited.add(temp3.toString());
	queue.add(temp3);
	}
	Node temp4 = new Node(temp);
	temp4.b = decremet(temp.b);
	if(!deadEnd.contains(temp4.toString()) && !visited.contains(temp4.toString()))
	{
	//System.out.println(temp4);
	visited.add(temp4.toString());
	queue.add(temp4);
	}
	// c updated
	Node temp5 = new Node(temp);
	temp5.c = increment(temp.c);
	if(!deadEnd.contains(temp5.toString()) && !visited.contains(temp5.toString()))
	{
	//System.out.println(temp5);
	visited.add(temp5.toString());
	queue.add(temp5);
	}
	Node temp6 = new Node(temp);
	temp6.c = decremet(temp.c);
	if(!deadEnd.contains(temp6.toString()) && !visited.contains(temp6.toString()))
	{
	// System.out.println(temp6);
	visited.add(temp6.toString());
	queue.add(temp6);
	}
	// d updated
	Node temp7 = new Node(temp);
	temp7.d = increment(temp.d);
	if(!deadEnd.contains(temp7.toString()) && !visited.contains(temp7.toString()))
	{
	//System.out.println(temp7);
	visited.add(temp7.toString());
	queue.add(temp7);
	}
	Node temp8 = new Node(temp);
	temp8.d = decremet(temp.d);
	if(!deadEnd.contains(temp8.toString()) && !visited.contains(temp8.toString()))
	{
	//System.out.println(temp8);
	visited.add(temp8.toString());
	queue.add(temp8);
	}
	}
	level++;
	}
	return -1;
	}
	private int decremet(int a)
	{
	return (a+10-1)%10;
	}
	private int increment(int a)
	{
	return (a+1)%10;
	}
	}

view raw OpenTheLock.java hosted with by GitHub