To be frank, as I read the problem I realized it is a BFS problem. Let’s see what was my thought, we have to count the number of steps to reach the final string, this denotes we have to traverse the intermediate nodes. We cannot directly jump to the final string and apply some formula to get minimum steps. My second thought was can I change the final string and try to reach “0000”. We can try this but finding the minimum number of steps from this approach is difficult.
Finding a minimum number of steps from one position to another which has intermediate states, BFS was my next thought.
Given a string with 4 characters where each character is between 0-9. So there are 10^4 possibilities. To convert a problem to a graph problem we want Nodes and Edges. Let’s convert this to a graph problem by denoting a single string as a Node. i.e “0000” is one Node, “1000” another.
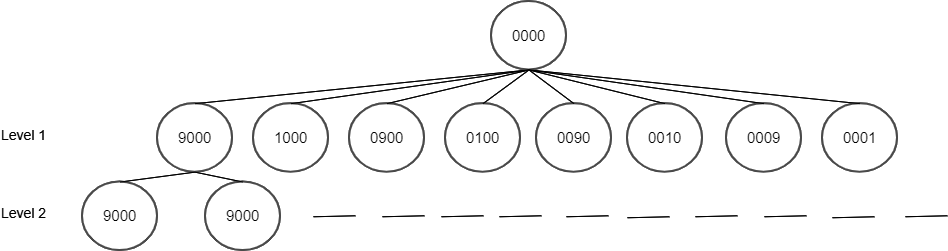
In step 1 we can reach all the nodes in Level 1, in 2 steps all the Nodes in level 2. This is a BFS, we have to find at what level our target Node is present and avoid visiting the already visited node. Along with that, the problem statement provides some Nodes as Invalid. We should not traverse these nodes further.